Soal Latihan Sumatif Akhir Semester Genap Kelas VIII Kurikulum Merdeka

Penilaian akhir semester (PAS) atau yang sekarang disebut dengan sumatif akhir semester (SAS) merupakan salah satu bentuk penilaian yang dilakukan oleh guru untuk mengukur sejauh mana pemahaman siswa terhadap materi yang telah diajarkan selama satu semester.

Bagi siswa kelas VIII SMP yang menggunakan Kurikulum Merdeka, SAS merupakan kesempatan untuk mengukur pemahaman mereka terhadap materi matematika, bahasa Indonesia, bahasa Inggris, IPA, IPS, dan PJOK.

Untuk membantu siswa mempersiapkan diri menghadapi SAS, berikut ini kami sajikan soal latihan SAS kelas VIII Kurikulum Merdeka yang terdiri dari 50 soal pilihan ganda beserta pembahasannya.

Soal-soal latihan ini mencakup materi bilangan berpangkat, bentuk akar, bentuk baku, Relasi dan Fungsi, Persamaan Garis Lurus, dan Statistika.

Soal-soal latihan ini disusun berdasarkan kisi-kisi SAS kelas VIII Kurikulum Merdeka. Dengan demikian, soal-soal ini dapat menjadi gambaran tentang materi yang akan diujikan pada SAS.

Berikut ini adalah beberapa tips untuk mengerjakan soal latihan SAS:

Bacalah soal dengan cermat dan teliti.

Pahamilah maksud dari soal.

Pilihlah jawaban yang paling tepat.

Jika tidak yakin dengan jawaban, tinggalkan saja dan lanjutkan ke soal berikutnya.

Semoga soal latihan ini dapat membantu siswa kelas VIII SMP yang menggunakan Kurikulum Merdeka untuk mempersiapkan diri menghadapi SAS.

Soal 1

Relasi yang tepat dari diagram panah di bawah adalah …

A. kurang dari

B. lebih dari

C. akar dari

D. kuadrat dari

Pembahasan

C. akar dari

Soal 2

Untuk menyatakan suatu bentuk "relasi" dari dua buah himpunan dapat disajikan dalam beberapa cara, yaitu ...

A. Diagram Garis, Koordinat Cartesius, Pasangan berurutan

B. Diagram Panah, Koordinat Cartesius, Pasangan berurutan

C. Koordinat Cartesius,Diagram Panah, Penulisan berurutan

D. Diagram Panah, Koordinat Cartesius, Diagram Lingkaran

Pembahasan

B. Diagram Panah, Koordinat Cartesius, Pasangan berurutan

Soal 3

Relasi dari A ke B yang ditunjukkan dengan diagram Cartesius di bawah adalah …

A. kelipatan dari

B. faktor dari

C. kurang dari

D. sama dengan

Pembahasan

B. faktor dari

Soal 4

Diketahui himpunan A = {x| 4 ≤ x < 7, x himpunan bilangan genap}, dan B = {x| 1 ≤ x < 7, x ∈ himpunan bilangan ganjil} himpunan pasangan berurutan yang menyatakan relasi “lebih dari” himpunan A kehimpunan B adalah......

A. {(4,1), (4,3), (6,1), (6,3), (6,5)}

B. {(4,5)}

C. {(4,1), (6,5)}

D. {(4, 6, 1, 3, 5)}

Pembahasan

A = {x| 4 ≤ x < 7, x ∈ himpunan bilangan genap}

A = {4, 6}

B = {x| 1 ≤ x < 7, x ∈ himpunan bilangan ganjil}

B = {1, 3, 5}

Relasi A ke B "lebih dari" = {(4,1), (4,3), (6,1), (6,3), (6,5)}

Soal 5

P = {(Arni, IPS), (Arni, Olahraga), (Budi, Matematika), (Vino, IPA), (Vino, Bahasa Inggris)}. Relasi yang menjelaskan himpunan berpasangan tersebut adalah ......

A. Ibukota dari

B. Warna favorit

C. Mata pelajaran kesukaan

D. Film kesukaan

Pembahasan

C. Mata pelajaran kesukaan

Soal 6

Perhatikan diagram panah berikut! Aturan relasi yang sesuai dengan diagram panah di bawah adalah …

A. lebih dari

B. kurang dari

C. faktor dari

D. satu kurangnya dari

Pembahasan

D. satu kurangnya dari

Soal 7

Domain dari diagram panah di atas adalah ….

A. {1, 2, 3, 4}

B. {1, 2, 6}

C. {1, 6}

D. {3}

Pembahasan

A. {1, 2, 3, 4}

Soal 8

Aturan khusus yang memasangkan setiap anggota suatu himpunan dengan tepat satu anggota pada himpunan lain merupakan pengertian dari ....

A. Relasi

B. Fungsi

C. Korespondensi Satu-Satu

D. Domain

Pembahasan

B. Fungsi

Soal 9

Diagram panah di bawah ini yang merupakan fungsi dari himpunan P ke himpunan Q adalah ….

Pembahasan

Soal 10

Himpunan pasangan berurutan dari grafik cartesius di bawah adalah …

A. {(2, 1), (3, 5), (4, 4), (6, 4)}

B. {(1, 2), (2, 4), (4, 6), (5, 3)}

C. {(1, 2), (2, 4), (4, 4), (4, 6), (5, 3)}

D. {(2, 1), (3, 5), (4, 2), (4, 4), (6, 4)}

Pembahasan

D. {(2, 1), (3, 5), (4, 2), (4, 4), (6, 4)}

Soal 11

Range dari gambar diagram panah di bawah adalah ...

A. {0, 2, 4, 6}

B. {1, 2, 3, 4}

C. {2, 4}

D. {0, 6}

Pembahasan

Range = {2, 4}

Soal 12

Pernyataan yang benar sesuai dengan diagram panah di bawah adalah …

A. Domain = {1, 2, 3}

B. Kodomain = {a, c, d}

C. Range = {a, c, d}

D. Bayangan = {b, e}

Pembahasan

Range = {a, c, d}

Soal 13

Diketahui P = {a, b, c, d} dan Q = {1, 2, 3}. Banyaknya pemetaan yang mungkin dari himpunan Q ke himpunan P adalah ….

A. 7

B. 12

C. 64

D. 81

Pembahasan

n(P) = 4

n(Q) = 3

Banyak Pemetaan himpunan Q ke himpunan P = $n(P)^n(Q)$

= $4^3$

= 64

Soal 14

Diketahui himpunan P = {x| x < 5, x ϵ bilangan asli} dan Q = {bilangan ganjil yang kurang dari 7}, banyak pemetaan yang mungkin dibuat dari himpunan P ke himpunan Q adalah …

A. 81

B. 125

C. 256

D. 625

Pembahasan

P = {x| x < 5, x ϵ bilangan asli}

P = {1, 2, 3, 4}

Q = {bilangan ganjil yang kurang dari 7}

Q = {1, 3, 5}

n(P) = 4

n(Q) = 3

Banyak Pemetaan himpunan P ke himpunan Q = $n(Q)^n(P)$

= $3^4$

= 81

Soal 15

Diketahui f(x) = 2x + 1. Jika daerah asalnya ={-1,0,1}, maka daerah hasil fungsinya adalah ....

A. {-3,1,3}

B. {-1,0,1}

C. {-1,1,3}

D. {0,1,2}

Pembahasan

f(x) = 2x + 1

f(-1) = 2(-1) + 1 = -2 + 1 = -1

f(0) = 2(0) + 1 = 0 + 1 = 1

f(1) = 2(1) + 1 = 2 + 1 = 3

Range = {-1, 1, 3}

Soal 16

Diketahui f(x) = -2x + 7, nilai dari f(-2) adalah …

A. 3

B. 4

C. 7

D. 11

Pembahasan

f(x) = -2x + 7

f(-2) = 2(-2) + 7 = -4 + 7 = 3

Soal 17

Diketahui rumus fungsi f(x) = 3x+7. Jika f(a)=13, maka nilai a adalah ....

A. 1

B. 2

C. 3

D. 4

Pembahasan

f(x) = 3x + 7

f(a) = 13

3a + 7 = 13

3a = 13 - 7

3a = 6

a = 2

Soal 18

Diketahui fungsi f : x → 2x + 5, jika f(a) = 35, maka nilai a adalah …

A. 11

B. 13

C. 15

D. 20

Pembahasan

f(x) = 2x + 5

f(a) = 35

2a + 5 = 35

2a = 35 - 5

2a = 30

a = 15

Soal 19

Diketahui fungsi f(x) = px + q, Jika f(7) = 23 dan f(3) = 11. Maka rumus fungsi dari f(x) adalah …

A. f(x) = 23x + 11

B. f(x) = 2x + 3

C. f(x) = 7x + 3

D. f(x) = 3x + 2

Pembahasan

f(x) = px + q

f(7) = 23 => 7p + q = 23

f(3) = 11 +> 3p + q = 11 -

4p = 12

p = 3

Substitusi p = 3 ke 7p + q = 23

7(3) + q = 23

21 + q = 23

q = 23 - 21

q = 2

Jadi, f(x) = 3x + 2

Soal 20

Fungsi f ditentukan dengan rumus f(x)= ax+b. Bila f(2)=1 dan f(4)=7, maka nilai a+2b adalah .....

A. -13

B. -12

C. -7

D. 7

Pembahasan

f(x) = ax + b

f(2) = 1 => 2a + b = 1

f(4) = 7 => 4a + b = 7 -

-2a = - 6

a = 3

Substitusi a = 3 ke 2a + b = 1

2(3) + b = 1

6 + b = 1

b = 1 -6

b = -5

Jadi, a + 2b = 3 + 2(-5) = 3 - 10 = -7

Soal 21

Diketahui fungsi f : x → 3x + 4. Jika domain fungsi adalah D = {-2, -1, 0, 1} dan kodomainnya adalah bilangan bulat, maka range fungsi tersebut adalah …

A.{-2, 1, 4, 7}

B. {1, 2, 4, 7}

C. {4, 7, 10}

D. {-1, 0, 4, 7}

Pembahasan

f(x) = 3x + 4

f(-2) = 2(-2) + 4 = -4 + 4 = 0

f(-1) = 2(-1) + 4 = -2 + 4 = 2

f(0) = 2(0) + 4 = 0 + 4 = 4

f(1) = 2(1) + 4 = 2 + 4 = 6

Range = {0, 2, 4, 6}

Soal 22

1. Siswa dengan Nomer Induk Siswa Nasional

2. Siswa dengan ukuran sepatunya

3. Siswa dengan sidik jarinya

4. Siswa dengan tanggal lahirnya

Dari pernyataan di atas yang merupakan korespondensi satu-satu adalah pernyataan ….

A. 1 dan 2

B. 1 dan 3

C. 2 dan 4

D. 3 dan 4

Pembahasan

B. 1 dan 3

Soal 23

Pasangan himpunan di bawah ini yang dapat membentuk korespondensi satu-satu adalah....

A. A = {lima bilangan asli yang pertama} dan B = {bilangan prima kurang dari 15}

B. A = {g, e, l, a, s} dan B = {huruf pembentuk kata "HABITAT"}

C. A = {huruf vokal} dan B = {huruf pembentuk kata "LALAT"}

D. A = {x | x ≤ 3, x ∈ bilangan asli} dan B = {x | -2 < x ≤ 3, x ∈ bilangan bulat}

Pembahasan

B. A = {g, e, l, a, s} dan B = {huruf pembentuk kata "HABITAT"}

Soal 24

Jika A = {x| 0 < x ≤ 4, x ∈ bilangan cacah} dan B = {faktor positif dari 6}, banyak korespondensi satu-satu yang mungkin adalah....

A. 6

B. 24

C. 120

D. 720

Pembahasan

A = {x| 0 < x ≤ 4, x ∈ bilangan cacah}

A = {1, 2, 3, 4}

n(A) = 4

B = {faktor positif dari 6}

B = {1, 2, 3, 6}

n(B) = 4

Banyak korespondensi satu-satu = 4! = 4 x 3 x 2 x 1 = 24

Soal 25

Diketahui himpunan M = {x | x ≤ 5, x ϵ bilangan cacah} dan himpunan N = {x | x < 17, x ϵ bilangan prima}. Banyaknya korespondensi satu-satu yang mungkin dibuat dari kedua himpunan adalah …

A. 120

B. 720

C. 5040

D. 40320

Pembahasan

M = {x | x ≤ 5, x ϵ bilangan cacah}

M = {0, 1, 2, 3, 4, 5}

n(M) = 6

N = {x | x < 17, x ϵ bilangan prima}

N = {2, 3, 5, 7, 11, 13}

n(N) = 6

Banyak korespondensi satu-satu = 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720

Soal 26

Diketahui :

P = {(1,1), (1,2), (2,2), (3,3)}

Q = {(1,1), (2,3), (3,3), (4,1)}

R = {(1,1), (2,3), (3,4), (4,5)}

S = {(1,1), (2,3), (3,3), (3,4)}

Himpunan pasangan berurutan di atas, yang merupakan fungsi adalah ….

A. P dan R

B. Q dan R

C. R dan S

D. S dan P

Pembahasan

B. Q dan R

Soal 27

27. Himpunan pasangan berurutan berikut ini yang merupakan korespodensi satu-satu adalah ....

A. {(1, 3), (2, 4), (1, 7), (9, 3)}

B. {(1, 3), (2, 5), (3, 7), (4, 9)}

C. {(1, 3), (2, 3), (1, 7), (9, 7)}

D. {(1, 5), (1, 4), (2, 5), (3, 7)}

Pembahasan

B. {(1, 3), (2, 5), (3, 7), (4, 9)}

Soal 28

Suatu fungsi $f(x) = x^2 + 2x -3$. Nilai f(3) adalah …

A. 6

B. 9

C. 12

D. 15

Pembahasan

$f(x) = x^2 + 2x -3$

$f(3) = 3^2 + 2(3) - 3 = 9 + 6 - 3 = 12$

Soal 29

Diketahui fungsi f(x) = px + q, jika f(2) = 8 dan f(5) = 14, maka nilai dari f(-3) adalah …

A. -1

B. -2

C. -4

D. -6

Pembahasan

f(x) = px + q

f(2) = 8 => 2p + q = 8

f(5) = 14 => 5p + q = 14 -

-3p = - 6

p = 2

Substitusi p = 2 ke 2p + q = 8

2(2) + q = 8

4 + q = 8

q = 4

f(x) = 2x + 4

f(-3) = 2(-3) + 4 = -6 + 4 = -2

Soal 30

Suatu pabrik dapat menghasilkan semen sesuai fungsi f(x) = 1,5x + 3 ton, dimana x merepresentasikan banyak bahan baku yang digunakan dalam satuan ton. Jika bahan baku yang digunakan adalah 200 ton, banyak semen yang dihasilkan adalah …

A. 300,00 ton

B. 303,00 ton

C. 303,50 ton

D. 306,50 ton

Pembahasan

f(x) = 1,5 x + 3

f(200) = 1,5(200) + 3 = 300 + 3 = 303,00 ton

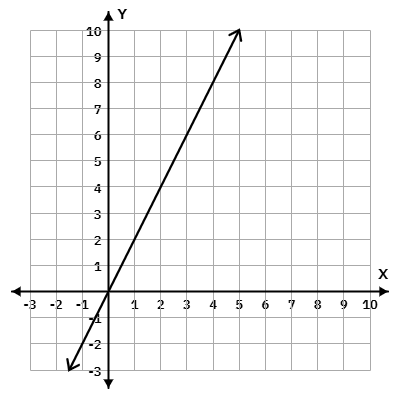
Soal 31

Grafik persamaan garis lurus y = -3x adalah …

Pembahasan

Dua titik sembarang dari y = -3x

x	-1	1
y	3	-3
(x, y)	(-1, 3)	(1, -3)

Sehingga gambar yang teat adalah

Soal 32

Grafik persamaan 3y-4x-12=0 adalah ...

Pembahasan

titik potong sumbu x dan sumbu y dari garis 3y - 4x - 12 = 0

titik potong sumbu x (y = 0)

3(0) - 4x - 12 = 0

0 - 4x = 12

-4x = 12

x = $\frac{12}{-4}$

x = -3

Jadi titik potong sumbu x = (-3, 0)

titik potong sumbu y (x = 0)

3y - 4(0) - 12 = 0

3y - 0 = 12

3y = 12

y = $\frac{12}{3}$

y = 4

Jadi titik potong sumbu y = (0, 4)

Sketsa grafik berdasarkan titik potong

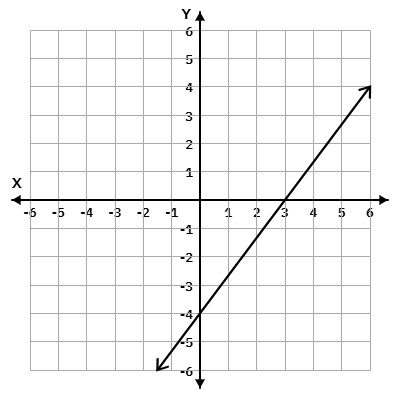
Soal 33

Perhatikan gambar berikut!

Gradien garis PQ adalah ...

A. -2

B. -1/2

C. 1/2

D. 2

Pembahasan

dari kiri ke kanan garis turun sehingga gradien negatif. Perubahan nilai y (vertikal) = 3, sedangkan perubahan nilai x (horisontal) = 6, jadi gradiennya

$m = -\frac{3}{6}$

$m = -\frac{1}{2}$

Soal 34

Perhatikan gambar berikut!

Gradien dari garis pada gambar adalah ...

A. m = -5/3

B. m = -3/5

C. m = 3/5

D. m = 5/3

Pembahasan

Ambil dua titik yang dilalui oleh garis dalam hal ini (3, 0) dan (0, -5)

$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$

$m = \frac{-5 - 0}{0 - 3}$

$m = \frac{-5}{-3}$

$m = \frac{5}{3}$

Soal 35

Gradien garis dengan persamaan 3x + 4y – 7 = 0 adalah …

A. m = -3/4

B. m = -4/3

C. m = -3/7

D. m = -4/7

Pembahasan

$m = -\frac{a}{b}$

$m = -\frac{3}{4}$

Soal 36

Gradien garis yang melewati titik asal (3, 4) dan titik (4, -1) adalah …

A. m = -5

B. m = -1/5

C. m = 1/5

D. m = 5

Pembahasan

$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$

$m = \frac{-1 - 4}{4 - 3}$

$m = \frac{-5}{1}$

$m = -5$

Soal 37

Gradien dari dua garis yang saling sejajar memiliki sifat …

A. m₁ = m₂

B. m₁ + m₂ = -1

C. m₁ x m₂ = -1

D. m₁ x m₂ = 1

Pembahasan

A. m₁ = m₂

Soal 38

Persamaan garis yang melalui titik (-4, 5) dengan gradien -3 adalah …

A. y = -3x + 7

B. y = -3x - 7

C. y = 3x + 7

D. y = 3x - 7

Pembahasan

Persamaan garis yang melalui titik (-4, 5) dengan gradien -3

$y - y_{1} = m(x - x_{1})$

y - 5 = (-3)(x - (-4))

y - 5 = -3(x + 4)

y - 5 = -3x - 12

y = -3x - 12 + 5

y = -3x - 7

Soal 39

Perhatikan gambar berikut!

Persamaan garis pada gambar di atas adalah ...

A. 4x + 5y = -20

B. 4x - 5y = 20

C. -4x + 5y = 20

D. 4x + 5y = 20

Pembahasan

Dua titik yang dilalui garis (5, 0) dan (0, 4), sehingga persamaan garisnya

$\frac{y - y_{1}}{y_{2} - y_{1}}=\frac{x - x_{1}}{x_{2} - x_{1}}$

$\frac{y - 0}{4 - 0}=\frac{x - 5}{0 - 5}$

$\frac{y }{4 }=\frac{x - 5}{- 5}$

$-5y = 4x - 20$

$-4x - 5y = -20$

$4x + 5y = 20$

Soal 40

Titik koordinat (3, 5) dan (6, 7) dapat membentuk suatu garis lurus yang memiliki persamaan ....

A. 2x + 3y - 9 = 0

B. 2x - 3y + 9 = 0

C. -2x + 3y + 9 = 0

D. 2x + 3y + 9 = 0

Pembahasan

Dua titik yang dilalui garis (3, 5) dan (6, 7), sehingga persamaan garisnya

$\frac{y - y_{1}}{y_{2} - y_{1}}=\frac{x - x_{1}}{x_{2} - x_{1}}$

$\frac{y - 5}{7 - 5}=\frac{x - 3}{6 - 3}$

$\frac{y - 5 }{2 }=\frac{x - 3}{3}$

$3y - 15 = 2x - 6$

$2x - 3y -6 + 15 = 0$

$2x - 3y + 9 = 0$

Soal 41

Persamaan garis lurus yang tegak lurus garis 3x + 2y – 7 = 0 dan melalui titik (3, 2) adalah …

A. 3x - 2y + 5 = 0

B. 3x + 2y - 5 = 0

C. -3x - 2y - 5 = 0

D. 3x - 2y - 5 = 0

Pembahasan

Gradien persamaan 3x + 2y - 7 = 0 adalah

$m_{1} = -\frac{a}{b}$

$m_{1} = -\frac{3}{2}$

Karena tegak lurus gradien garis yang dicari $m_{2}$

$m_{1} \times m_{2} = -1$

$-\frac{3}{2} \times m_{2} = -1$

$m_{2} = \frac{2}{3}$

Persamaan garis dengan gradien $m_{2} = \frac{3}{2}$ dan melalui (3, 2) adalah

$y - y_{1} = m_{2}(x - x_{1})$

y - 2 = \frac{3}{2}(x - 3)

2y - 4 = 3(x - 3)

2y - 4 = 3x - 9

3x - 2y -9 + 4 = 0

3x - 2y - 5 = 0

Soal 42

Persamaan garis Persamaan garis yang melalui titik (-3, 5) dan sejajar dengan garis yang melalui titik y = -2x - 5 adalah …

A. y = -2x + 1

B. y = 2x - 1

C. y = -2x - 1

D. y = 2x + 1

Pembahasan

Gradien persamaan y = -2x - 5 adalah

$m_{1} = -2$

Karena sejajar maka gradien garis yang dicari $m_{2}$

$m_{2} = m_{1}$

$m_{2} = -2$

Persamaan garis dengan gradien $m_{2} = -2$ dan melalui (-3, 5) adalah

$y - y_{1} = m_{2}(x - x_{1})$

$y - 5 = (-2)(x - (-3))$

$y - 5 = -2x - 6$

$y = -2x - 6 + 5$

$y = -2x - 1$

Soal 43

Data berikut: 5, 8, 6, 7, 8, 9, 8, 5, 10. Modus dari data tersebut adalah...

A. 8

B. 7

C. 6

D. 5

Pembahasan

A. 8

Soal 44

Berikut adalah data berat badan (dalam kg) dari delapan orang: 50, 62, 55, 58, 60, 53, 57, 65. Median dari data berat badan tersebut adalah...

A. 56

B. 57

C. 57,5

D. 58

Pembahasan

Data diurutkan

50, 53, 55, 57, 58, 60, 62, 65

Median data genap

$Me = \frac{57 + 58}{2}$

$Me = 57,5$

Soal 45

Nilai ulangan matematika dari 7 siswa adalah 4, 2, 8, 5, 6, a, 9. Jika rata-ratanya 6 maka nilai a adalah ....
A. 6
B. 7
C. 8
D. 9

Pembahasan

$\overline{x}=\frac{x_{1}+x_{2}+x_{3}+...+x_{n}}{n}$

$6 =\frac{4+2+8+5+6+a+9}{7}$

$6 =\frac{34+a}{7}$

$6\times7=34+a$

$42=34+a$

$42-34=a$

$a = 8$

Soal 46

Jangkauan dari data 3, 6, 10, 5, 8, 9, 6, 4, 7, 5, 6, 9, 5, 2, 4, 7, 8 adalah ...

A. 7

B. 8

C. 9

D. 10

Pembahasan

Jangkauan = 10 - 2 = 8

Soal 47

Perhatikan tabel nilai Matematika di bawah! Banyak siswa yang memperoleh nilai di atas rata-rata adalah …

A. 9 orang

B. 12 orang

C. 16 orang

D. 24 orang

Pembahasan:

$\overline{x}= \frac{4\times5+5\times6+7\times7+13\times8+6\times9+5\times10}{4+5+7+13+6+5}$

$\overline{x}= \frac{20+30+49+104+54+50}{40}$

$\overline{x}= \frac{307}{40}$

$\overline{x}= 7,675$

Banyak siswa yang nilainya di atas 7,675 adalah 13+6+5 = 24 orang

Soal 48

Suatu kelas terdapat 40 siswa yang terdiri dari 24 wanita dan 16 pria. Rata-rata nilai siswa wanita 70 dan rata-rata nilai siswa pria 85. Rata-rata kelasnya adalah …

A. 74

B. 75

C. 76

D. 78

Pembahasan:

$\overline{x}_{gab}=\frac{n_{1}\overline{x}_{1}+n_{2}\overline{x}_{2}}{n_{1}+n_{2}}$

$\overline{x}_{gab}=\frac{24\times70+16\times85}{24+16}$

$\overline{x}_{gab}=\frac{1680+1360}{40}$

$\overline{x}_{gab}=\frac{3040}{40}$

$\overline{x}_{gab}=76$

Soal 49

Kuartil atas dari data: 5, 5, 7, 7, 6, 8, 7, 8, 9 adalah....

A. 5,5

B. 6

C. 6,5

D. 8

Pembahasan

Data diurutkan menjadi

5, 5, 6, 7, 7, 7, 8, 8, 9

$Q_{3} = 8$

Soal 50

Diberikan data sebagai berikut: 80, 81, 82, 83, 85, 86, 88. Jangkauan kuartil dari data di atas adalah....

A. 2

B. 3

C. 4

D. 5

Pembahasan

Data diurutkan menjadi

80, 81, 82, 83, 85, 86, 88

$Q_{1} = 81$

$Q_{3} = 86$

Jangkauan Kuartil $Q_{R}$

$Q_{R} = 86-81 = 5$

Soal latihan SAS kelas VIII Kurikulum Merdeka ini dapat dijadikan sebagai bahan latihan untuk mengukur pemahaman siswa terhadap materi yang telah dipelajari selama satu semester. Dengan mengerjakan soal-soal latihan ini, siswa dapat mengetahui materi apa saja yang masih perlu dipelajari dengan lebih mendalam.

Selain itu, soal latihan ini juga dapat membantu siswa untuk mempersiapkan diri menghadapi SAS. Dengan mengerjakan soal-soal latihan ini, siswa akan lebih terbiasa dengan format soal SAS dan dapat mengerjakan soal dengan lebih cepat dan tepat.

Semoga soal latihan SAS kelas VIII Kurikulum Merdeka ini dapat bermanfaat bagi siswa kelas VIII SMP yang akan menghadapi SAS.